HDOJ4489——国王的沉浮

问题描述

HDOJ4489
有n个身高递增的人，使他们高低高低排列，求一共有多少种排法。

或者

Input

The first line of input contains a single integer P, (1 <= P <= 1000), which is the number of data sets that follow. Each data set consists of single line of input containing two integers. The first integer, D is the data set number. The second integer, n (1 <= n <= 20), is the number of guards of differing heights.

Output

For each data set there is one line of output. It contains the data set number (D) followed by a single space, followed by the number of up and down orders for the n guards.

Sample Input

4
1 1
2 3
3 4
4 20

Sample Output

1 1
2 4
3 10
4 740742376475050

问题分析

这道题用组合排序的思想就比较简单，考虑有n个人的队列时，第n个人an一定比前面n-1个人都高。将他插入前n-1个人组成的队列之中，使得新的队列依旧满足题意，那么必须满足: an 的前面为下降的，an 的后面为上升的。如图。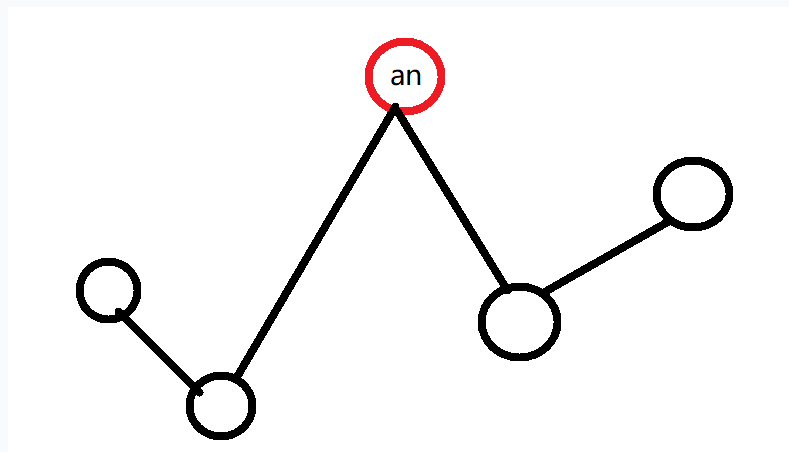

设an在n个人的队列中的位置为i，则他左边有i-1个人，他右边有n-i个人。容易推出这个时候所有的排列方法为$\frac{dp[i-1]}{2} \frac{dp[n-i]}{2} C{n-1}^{i-1}$
解释一下这个式子:左边i-1个人排出最右边为下降的队列的方法是总方法的一半，右边n-i个人同理，证明略。
那么n个人的总排序方法就是$\sum^{n}{i=1} \frac{dp[i-1]}{2} \frac{dp[n-i]}{2} C_{n-1}^{i-1} $

代码实现

#include<cstdio>
#include<cstring>
typedef long long LL;
LL c[21][21];
LL dp[21];
void pre()
{
  int i,j;
  /*求出C[0][0]到C[20][20]的组合数*/
  for(i=0;i<=20;i++)  c[0][i] = c[i][i] = 1;
  for(i=2;i<=20;i++)
    for(j=1;j<i;j++) c[j][i] = c[j-1][i-1] + c[j][i-1];
  dp[0] = dp[1] = 1;
  for(i=2;i<=20;i++)
  {
    for(j=1;j<=i;j++)
    {
      dp[i] += c[j-1][i-1] * ((j-1<=1) ? 1 : dp[j-1] / 2) * ((i-j<=1) ? 1 : dp[i-j] / 2);
    }
  }
}

int main()
{
  int i,set,kase,num;
  pre();
  scanf("%d",&kase);
  while(kase--)
  {
    scanf("%d%d",&set,&num);
    printf("%d %I64d\n",set,dp[num]);
  }
}