二叉树

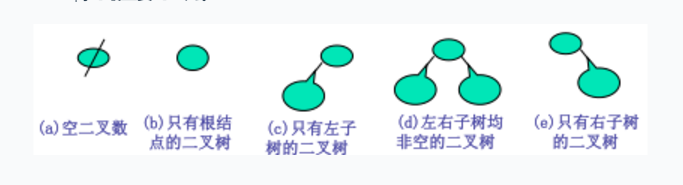
把满足以下两个条件的树型结构叫做二叉树（Binary Tree）：

1. 每个结点的度都不大于2；

2. 每个结点的孩子结点次序不能任意颠倒。即使只有一棵子树也要进行区分，说明它是左子树，还是右子树。这是二叉树与树的最主要的差别。

二叉树的性质

性质1： 在二叉树的第i层上至多有2^(i-1)个结点(i>=1)。

性质2 ：深度为 k 的二叉树至多有 2^k-1个结点(k≥1)。

性质3： 对任何一棵二叉树，如果其终端结点数为n0，度为2的结点数为n2，则n0＝n2＋1。

性质4：具有n个结点的完全二叉树的深度为[log2 n]＋1。

性质5： 如果对一棵有n个结点的完全二叉树的结点按层序编号（从第1层到第【log2n】+1层，每层从左到右),则对任一结点i（1<=i<=n),有：

1）如果i＝1，则结点i无双亲，是二叉树的根；如果i>1，则其双亲是结点【i/2】。

2）如果2i>n，则结点i为叶子结点，无左孩子；否则，其左孩子是结点2i。

3）如果2i＋1>n，则结点i无右孩子；否则，其右孩子是结点2i＋1。

两类特殊的二叉树：满二叉树和完全二叉树

满二叉树：一棵深度为k且有2^k-1个结点的二叉树。

完全二叉树：树中所含的 n 个结点和满二叉树中编号为 1 至 n 的结点一一对应。（编号的规则为，由上到下，从左到右。）

二叉树的存储结构

—- 二叉树是非线性结构，其存储结构可以分为两种，即顺序存储结构和链式存储结构。

1. 顺序存储结构

用一维数组来记录树的各个节点，它们之间的关系可以通过数学公式求得。

依据二叉树的性质，完全二叉树和满二叉树采用顺序存储比较合适，树中结点的序号可以唯一地反映出结点之间的逻辑关系，这样既能够最大可能地节省存储空间，又可以利用数组元素的下标值确定结点在二叉树中的位置，以及结点之间的关系。

—- 一棵完全二叉树（满二叉树）如下图所示：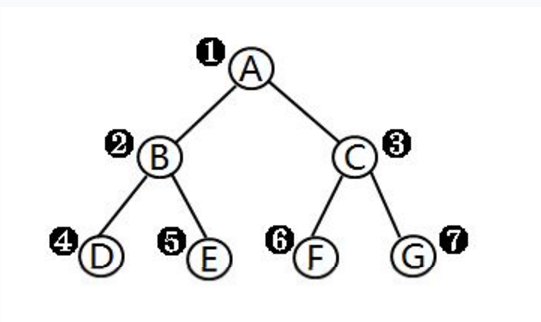

数组内的情况

对于非完全二叉树来说，可以对不存在的节点标定特殊值，说明这里没有节点。但是总而言之，这一种存储方式还是会浪费大量空间。

2.链式存储结构

typedef struct bnode  
{  
    char data;  
    struct bnode *lchild,*rchild;  
}B,*BTree;