二分图 最小覆盖数、最大匹配数与最大独立集
二分图 最小覆盖数、最大匹配数与最大独立集
定义
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
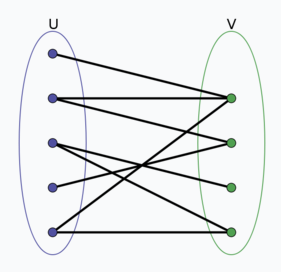
无向图G为二分图的充分必要条件是,G至少有两个顶点,且其所有回路的长度均为偶数。证明略
二分图判定方法
用可以用涂色法来判定一个图是否为二分图。
首先选中一个点,将其标为白色,然后将它邻接的点标为黑色。如果在这些邻接点中,有一个点为白色,则说明这个图不是二分图。s
二分图有几个问题,最常见的就是求最小覆盖数问题、最大匹配数问题和最大独立集问题。
这里给出其中定义
几个基本定义:
最小覆盖:即在所有顶点中选择最少的顶点来覆盖所有的边。
最大匹配:二分图左右两个点集中,选择有边相连的两个匹配成一对(每个点只能匹配一次),所能达到的最大匹配数。
最大独立集:集合中的任何两个点都不直接相连。
还有一个概念是DAG的最小路径覆盖,就是通过最少的节点,可以连接一张图所有的路径。最小路径覆盖包含最小不想交路径
覆盖和最小相交路径覆盖,其本质还是一样的。
这四个问题可以转化:
最小覆盖数 = 最大匹配数
最大独立集 = 总数-最小覆盖集
最小路径覆盖 = 最大独立集
最大匹配数
求最大匹配数有两种算法,其中最经典的就是匈牙利算法。还有一种DK算法过于复杂,这里不提。
匈牙利算法很好理解,它就是通过回溯法,尽可能多的找到匹配。对于一个匹配a→b,如果b已经和其他点连接了,则我们优先考虑的是b能否腾出位置让a来连,如果可以,则b和a匹配,b原先匹配点的继续和其他点重复这一过程。
算法模板
//匈牙利算法求最大匹配数
#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 256;
int n,m,k; //两个点集和边数
int mat[maxn][maxn],vis[maxn],cur[maxn];
bool find(int node)
{
for(int i=1;i<=n;i++)
{
if(mat[node][i] && !vis[i]) //i没有被访问过
{
vis[i] = 1;
if(!cur[i] || find(cur[i])) //如果i没有被连接或者i可以腾出位置
{
cur[i] = node; //i与node相连接
return true;
}
}
}
return false;
}
int main()
{
int a,b,sum = 0;
cin >> n >> m >> k;
for(int i=0;i<k;i++)
{
cin >> a >> b;
mat[a][b] = 1;
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(find(i)) sum ++;
}
cout << sum << endl;
}
例题选讲
HDOJ1281 —— 棋盘游戏
小希和Gardon在玩一个游戏:对一个N*M的棋盘,在格子里放尽量多的一些国际象棋里面的“车”,并且使得他们不能互相攻击,这当然很简单,但是Gardon限制了只有某些格子才可以放,小希还是很轻松的解决了这个问题(见下图)注意不能放车的地方不影响车的互相攻击。
所以现在Gardon想让小希来解决一个更难的问题,在保证尽量多的“车”的前提下,棋盘里有些格子是可以避开的,也就是说,不在这些格子上放车,也可以保证尽量多的“车”被放下。但是某些格子若不放子,就无法保证放尽量多的“车”,这样的格子被称做重要点。Gardon想让小希算出有多少个这样的重要点,你能解决这个问题么?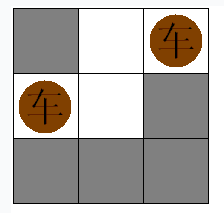
分析
虽然可以用DFS做,但是有一种巧妙的方法可以将其转换成一个二分图问题。
首先我们将长和宽作为二分图两边的点集,可以建立一张二分图。在能放置棋子的地方连一条边。
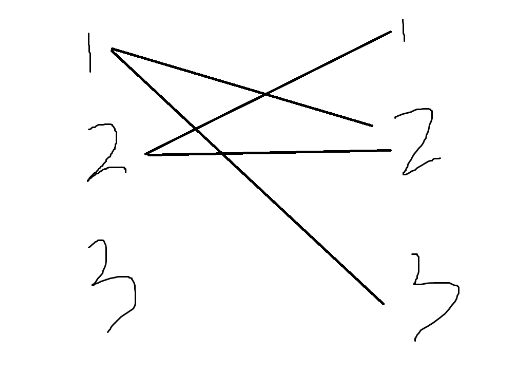
如图,那么每条边就代表这个坐标可以放置棋子。如果我们在某一个位置放置棋子,那么就选取这条边,显然与这个点同行或者同列的地方就不能放置棋子了,转化为二分图的意思就是:在选取一条边后,这条边的两个点不能再连其他边了。于是便转化成了一个最大匹配问题,直接上匈牙利算法。
能放置棋子的最大数量解决了,我们遇到了一个难点——求重要点。所谓重要点,就是这个地方若不放置棋子,最大匹配必然小。所以当我们第一次求出最大匹配之后,将匹配的边删去,重新做一次最大匹配。如果这一次最大匹配的数量减少了,说明这条边是重要边,这个点是重要点。
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int maxn = 100 + 10;
int max(int a,int b){return a>b?a:b;}
int n,m,k,kase;
int mat[maxn][maxn],vis[maxn],cur[maxn];
int count[maxn];
bool find(int node)
{
int i,cnt = 0;
for(i=1;i<=m;i++)
{
if(mat[node][i] && !vis[i])
{
vis[i] = 1;
if(!cur[i] || find(cur[i]))
{
cur[i] = node;
//return true;
cnt++;
}
}
}
if(cnt > 0)
{
count[node] = i;
return true;
}
else return false;
}
int main()
{
int a,b,sum,imp;
while(cin >> n >> m >> k)
{
memset(vis,0,sizeof(vis));
memset(cur,0,sizeof(cur));
vector<int> vec;
sum = 0;
while(k--)
{
cin >> a >> b;
mat[a][b] = 1;
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(find(i))
{
sum ++;
//vec.push_back(i);
}
}
imp = sum;
for(int i=0)
printf("Board %d have %d important blanks for %d chessmen.\n",++kase,imp,sum);
}
}
HDOJ1507——Uncle Tom’s Inherited Land*
如图,给出一个NM的方阵,白色的地方可以放置12的方块,求在一张图中最多能放置的方块数量,并输出位置。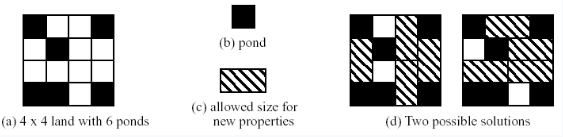
分析
因为是12的方格,所以可以看成是11和1*1的两个方格连在一起。将方阵看成国际象棋的棋盘,那么黑色的方格必然只能和白色方格相邻。事先对所有空的方格做标记,将所有空的(可放置的)黑色的方格放在一起,所有空的白色的方格放在一起,枚举每一个空的黑色方格的四个方向,如果某个方向的方格是空的,就在这两个方格之间连边。然后在得到的二分图中做最大匹配,记录匹配到的方格并输出。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<map>
#include<vector>
#include<string>
using namespace std;
const int maxn = 550 + 10;
typedef pair<int,int> P;
vector<int> b,w;
vector<int> out;
int n,m,k,cnt,flag;
int mat[110][110],vis[maxn],cur[maxn];
map<P,int> mp; //存储二分图连边的情况
int dir[4][2] = {{-1,0},{0,-1},{1,0},{0,1}};
bool find(int node)
{
for(int i=0;i<w.size();i++)
{
if(!vis[w[i]] && mp[P(node,w[i])])
{
vis[w[i]] = 1;
if(!cur[w[i]] || find(cur[w[i]]))
{
cur[w[i]] = node;
return true;
}
}
}
return false;
}
void conn(int y,int x) //枚举四个方向,连边
{
for(int i=0;i<4;i++)
{
int ny = y + dir[i][0];
int nx = x + dir[i][1];
if(ny < 1 || ny > n || nx < 1 || nx > m) continue;
if(mat[ny][nx])
{
mp[P(mat[y][x],mat[ny][nx])] = 1;
}
}
}
void solve()
{
int sum;
sum = 0;
for(int i=0;i<b.size();i++)
{
memset(vis,0,sizeof(vis));
if(find(b[i])) sum++;
}
for(int i=0;i<w.size();i++)
{
if(cur[w[i]]) out.push_back(w[i]); //如果匹配到,将其加入输出数组中
}
cout << sum << endl;
for(int i=0;i<out.size();i++) //输出
{
int y = (out[i] % m == 0) ? out[i] / m : out[i] / m + 1;
int x = (out[i] % m == 0) ? m : out[i] % m;
int ny = (cur[out[i]] % m == 0) ? cur[out[i]] / m : cur[out[i]] / m + 1;
int nx = (cur[out[i]] % m == 0) ? m : cur[out[i]] % m;
printf("(%d,%d)--(%d,%d)\n",y,x,ny,nx);
}
putchar('\n');
}
void init()
{
memset(mat,0,sizeof(mat));
memset(cur,0,sizeof(cur));
out.clear();
w.clear();
b.clear();
mp.clear();
int cnt = 0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
mat[i][j] = ++cnt;
}
int main()
{
int x,y,sum;
while(cin >> n >> m && (n && m))
{
cnt = sum = 0;
init();
cin >> k;
while(k--)
{
cin >> y >> x;
mat[y][x] = 0;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(mat[i][j])
{
if((i+j) & 1) w.push_back(mat[i][j]); //建立二分图
else
{
b.push_back(mat[i][j]);
conn(i,j);
}
}
}
solve();
}
}
HDOJ1151——Air Raid
题目链接
大意是有N个路口,某些路口之间有单行的街道,问至少空投几个士兵到不同的路口上,使得这些士兵可以走过所有的街道。
分析
这些路口和街道可以组成一个DAG(有向无环图),问题就是至少需要几个点就可以连出图里所有的边。这是一个经典的求最小路径覆盖问题,具体可以参考有向无环图(DAG)的最小路径覆盖。
最小路径覆盖有两种形态,这里给出简易做法:
1.不相交最小路径覆盖
不相交最小路径覆盖的意思是,找出的点连起来的边没有一条是重复的。做法是用图中所有点建立二分图,如果两个点之间有一条有向边,就连接二分图中两个点(从左往右连,作为方向),如图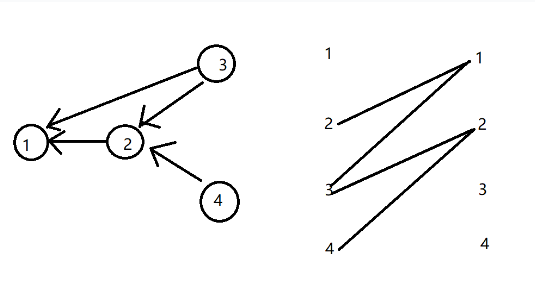
这里有一个公式,证明在上面的网址里..:
不相交最小路径覆盖 = 总节点数 - 最大匹配数
所以我们对画出来的二分图做最大匹配,就可以求出不相交最小路径覆盖啦~
2.相交最小路径覆盖
对于求相交最小路径覆盖覆盖类问题,对上面一种方法多了一个求传递闭包的工作。因为连边可以相交,所以实际上是限制变少了。对于一条路径1 -> 2 ->3 ->4,
我们可以直接找出路径1 -> 2 ,1 -> 3 ,1 -> 4,给这些节点都建上边,问题就转化成了不相交最小路径覆盖。 证明看上面的博客吧…
求传递闭包可以用floyd做
void floyd()
{
for(int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(mat[i][k] && mat[k][j])
mat[i][j] = 1;
}
}
所以,很容易看出这个题就是个求相交最小路径覆盖的模板题
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn = 128;
int n,k;
int mat[maxn][maxn],mp[maxn][maxn],vis[maxn],cur[maxn];
void floyd()
{
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(mat[i][k] && mat[k][j]) mat[i][j] = 1;
}
}
bool find(int node)
{
for(int i=1;i<=n;i++)
{
if(mp[node][i] && !vis[i])
{
vis[i] = 1;
if(!cur[i] || find(cur[i]))
{
cur[i] = node;
return true;
}
}
}
return false;
}
int main()
{
int kase,a,b,sum;
cin >> kase;
while(kase--)
{
sum = 0;
memset(mp,0,sizeof(mp));
memset(mat,0,sizeof(mat));
memset(cur,0,sizeof(cur));
cin >> n >> k;
while(k--)
{
cin >> a >> b;
mat[a][b] = 1;
}
floyd();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(mat[i][j]) mp[i][j] = 1;
}
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(find(i)) sum++;
}
cout << n - sum << endl;
}
}
