Graph Coloring

描述

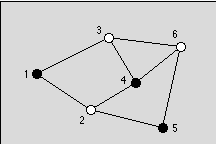
如图，我们可以给一幅图上色，要求黑色的颜色不能相邻。求问该如何上色，使得黑色的点最多？

问题分析

求不相邻的最大值——求一幅图的最大独立集。我们先建立图的补集，然后再求最大团。最大团的大小就是最多的点数量

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int maxn = 100 + 10;
int kase,n,m,best,num[maxn],mat[maxn][maxn];
vector<int> ans;

bool dfs(int *adj,int tot,int cnt,vector<int> vec)
{
  int i,j,k,t[maxn];
  if(tot == 0)
  {
    if(cnt > best)
    {
      ans = vec;
      best = cnt;
      return true;
    }
    else return false;
  }
  for(i=0;i<tot;i++)
  {
    if(cnt + (tot - i) <= best) return false;
    if(cnt + num[adj[i]] <= best) return false;
    for(k=0,j=i+1;j<tot;j++)
      if(mat[adj[i]][adj[j]]) t[k++] = adj[j];
    vec.push_back(adj[i]);
    if(dfs(t,k,cnt+1,vec))  return true;
    vec.pop_back();
  }
  return false;
}

int max_clique()
{
  int i,j,k,adj[maxn];
  vector<int> vec;
  if(n <= 0)  return 0;
  best = 0;
  for(i=n;i>0;i--)
  {
    for(k=0,j=i+1;j<=n;j++)
      if(mat[i][j]) adj[k++] = j;
    vec.push_back(i);
    dfs(adj,k,1,vec);
    num[i] = best;
    vec.pop_back();
  }
  return best;
}

int main()
{
  ios::sync_with_stdio(false);cin.tie(0);
  int a,b;
  cin >> kase;
  while(kase--)
  {
    memset(mat,1,sizeof(mat));
    cin >> n >> m;
    for(int i=0;i<m;i++)
    {
      cin >> a >> b;
      mat[a][b] = mat[b][a] = 0;
    }
    max_clique();
    cout << best << endl;
    for(int i=0;i<best;i++)
    {
      if(i == 0)  cout << ans[i];
      else cout << " " << ans[i];
    }
    if(best > 0)  cout << endl;
  }
}