搜索入门——DFS与BFS
搜索入门——DFS与BFS
MOOC后台第一次算法授课
0. 写在前面
部长竟然要求每个人都要抖点料出来…我明明啥都不会还非要写点什么。本来想写点关于STL的知识的,考虑到社团里好多人都不接触C++,而Java里好用的类比STL多太多了,作罢。算法也不会那么几个,姑且只能非常非常浅显地讲一下搜索的方法吧…
本文会把重心放在让你们明白搜索是个啥玩意儿,并不要求你们人人都会写(其实我也不怎么会写)…只能说,搜索是一种思想,而不是死的方法。接触多了你们会发现,万物皆可搜索(呸
这篇文章就浅显提了下DFS和单向BFS两种最基础的搜索算法…其实还有一些比如A*或者双向BFS之类的高端操作,但是我也不会(摊手)
1. 何为搜索
1.1 一个简单的问题
先举个例子,现在给你一张迷宫,用坐标标记出了你的位置,终点的位置,墙的位置和路的位置,要求设计一个程序,解决以下三个问题
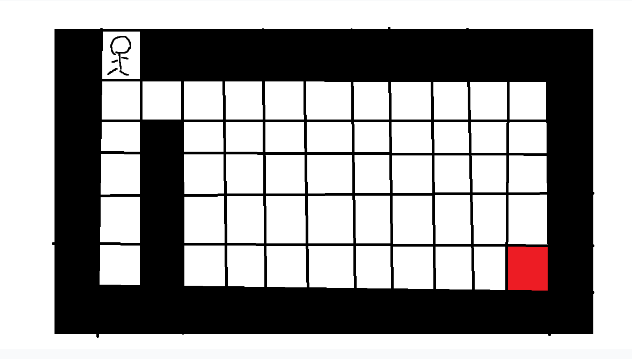
1.从起点出发能否到达终点
2.在有限时间内,能否从出发点到达终点
3.若能从起点出发到达终点,求出从起点到终点的最短路径的路程
…
如果你不会搜索,你会发现这类问题根本无从下手,即使你看一眼就明白答案是什么。
想想你是怎么通过”看”这个玄学操作得出答案的?实际上是你的大脑通过高速处理后,了解了在这个迷宫里,哪些路是死路,哪些路是通往终点的路,哪些路是相对比较近的路。所谓搜索,实际上就是让计算机模拟人脑的这个过程,但是计算机不知道从何开始看起,所以你需要帮助它制定一套搜索规则。如同网络爬虫一样,只要有一套搜索规则,就可以自主地在迷宫中进行探寻,把所有死路、可行路都找出来。
搜索算法的本质是一种暴力算法,它尽可能穷举一个问题的所有可能性,从而得到结论。
而你要做的,就是制定一套搜索规则,帮助计算机实现搜索这个过程。
在算法道路上,搜索是最基础、最容易掌握而又对你解决一系列问题有重大推动力的算法,所以请务必掌握。
1.2搜索的应用
前面之所以举迷宫的例子,是因为这类问题比较生动形象,容易讲,其实只是搜索的一个很浅显的应用…搜索广泛应用在数据结构之中,比如树和图的很多问题都要用到搜索。也许这篇文章对你理解搜索一点用都没有,但是我还是想告诉你:搜索很有用
2.DFS——深度优先搜索
2.1介绍一下全称吧
DFS全称是Deep First Search,翻译过来叫深度优先搜索。先顺便提一下,BFS的全称是Breath First Search,广度优先搜索。
从英文名或者中文名就可以看出两者区别。一个是一心一意,一直深入,直到有了成果或者把自己逼到无路可走。一个是广撒网多捞鱼,这里看看那里看看。
那么接下来进入正题。
2.2 算法实现
一般的DFS,我们用函数递归的方式实现。深度优先的原则是:只要还有路可以走,就一路走到底,直到无路可走再回溯上来。
拿之前的迷宫举例子。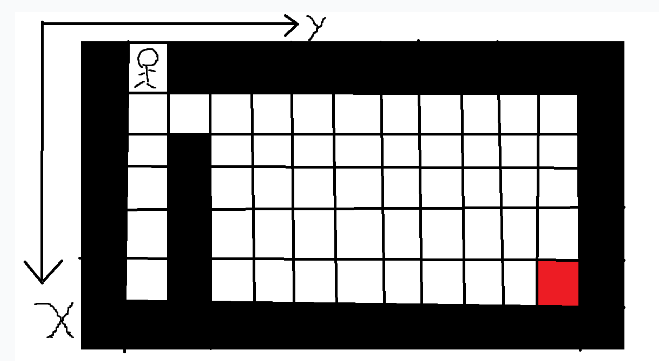
我们用二维数组记录地图数据,另外开一个数组记录地图的访问情况。
开一个dir数组,用来规定搜索的规则,这里以上左下右为顺序。
int mp[maxn][maxn]; //记录地图
int vis[maxn][maxn]; //记录地图的访问情况
dir[4][2] = {{-1,0},{0,-1},{1,0},{0,1}} // 这是上左下右的顺序
//地图可以向下面一样存,当然符号可以自己定
//* S * * * * * * * * * * *
//* . . . . . . . . . . . *
//* . * . . . . . . . . . *
//* . * . . . . . . . . . *
//* . * . . . . . . . . . *
//* . * . . . . . . . . E *
//* * * * * * * * * * * * *
用深度优先的顺序,小人会从起点S位置依次遍历上、左、下、右四个方向,一旦某个方向有路可走,就递归下去,同时做一个访问标记,说明这个格子已经走过了,之后不用再走回头路了。若无路可走了,函数会自动回溯到上一个状态,继续搜寻其他的路线。
按照上图的结构,小人会优先一直往下走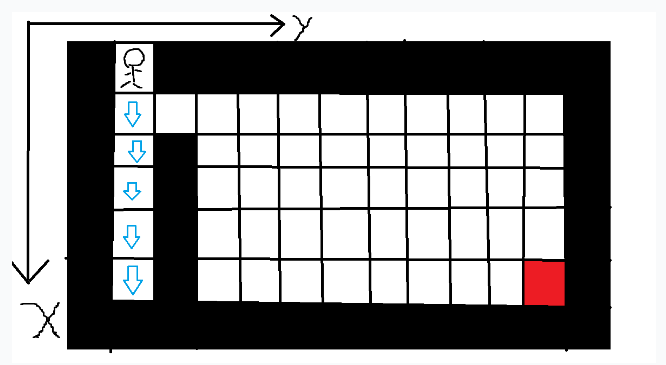
到达最下方时,判断上下左右都无路可走(上面的路由于已经被标记过了,不能再走)回溯到上移状态。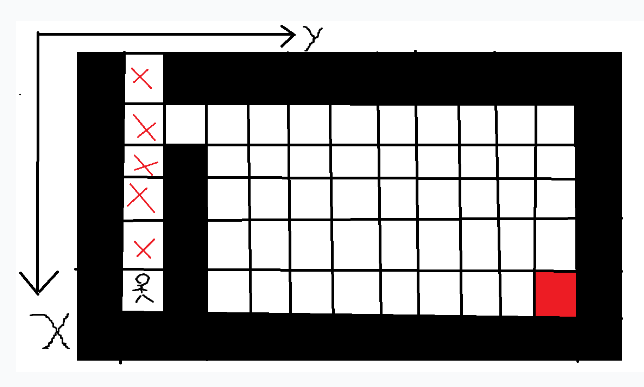
回溯
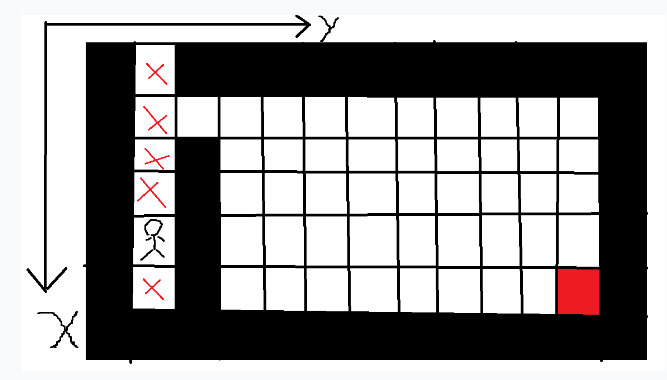
回溯完发现依然可走,所以继续回溯,直到有路为止。
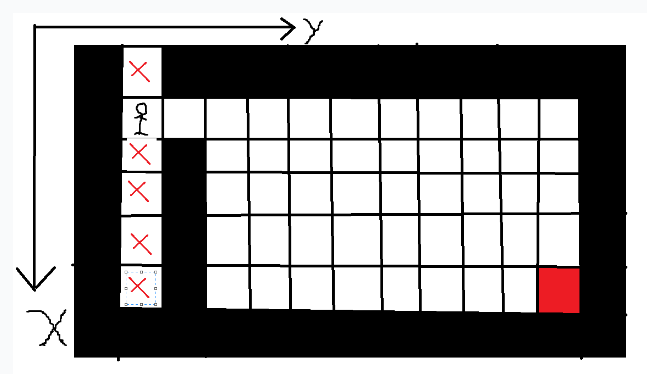
之后小人只能往右走,然后再往下走。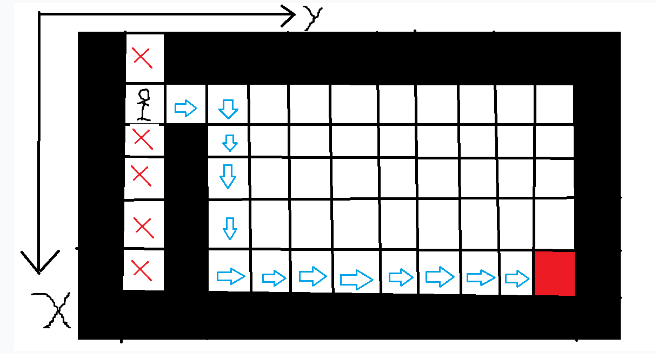
找到终点后,函数返回。
下面给出代码的形式
#include<iostream>
#include<cstring>
using namespace std;
const int maxn = 128; //地图的最大范围
char mp[maxn][maxn], vis[maxn][maxn];
int dir[4][2] = { {-1,0},{0,-1},{1,0},{0,1} };
int n,m; //地图规模为n * m
int sx, sy, ex, ey; //记录起点和终点的坐标
bool flag = false; //是否找到终点的标志
void dfs(int x, int y)
{
if (x == ex AND y == ey) //到达终点
{
flag = true;
return;
}
if (flag == false) //如果还没有找到终点,那就要继续递归下去找
{
for (int i = 0; i < 4; i++)
{
// 下一坐标的位置
int next_x = x + dir[i][0];
int next_y = y + dir[i][1];
if (next_x < 1 || next_x > n || next_y < 1 || next_y > m || vis[next_x][next_y] == 1)
continue; //如果下一坐标越界或者下一坐标已经访问过
if (mp[next_x][next_y] == '.')
{
vis[next_x][next_y] = 1;
dfs(next_x, next_y);
// vis[next_x][next_y] = 0; 标记的还原,某些情况下必须有,这里不需要
}
}
}
}
int main()
{
int sx, sy; //记录起点坐标
cin >> n >> m;
/*读入地图数据*/
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
{
cin >> mp[i][j];
if (mp[i][j] == 'S')
{
sx = i;
sy = j;
mp[i][j] = '.';
}
if (mp[i][j] == 'E')
{
ex = i;
ey = j;
mp[i][j] = '.';
}
}
memset(vis, 0, sizeof(vis)); // 初始化
flag = false;
dfs(sx, sy);
if (flag == true)
cout << "从起点可以到达终点" << endl;
else
cout << "从起点无法到达终点" << endl;
return 0;
}
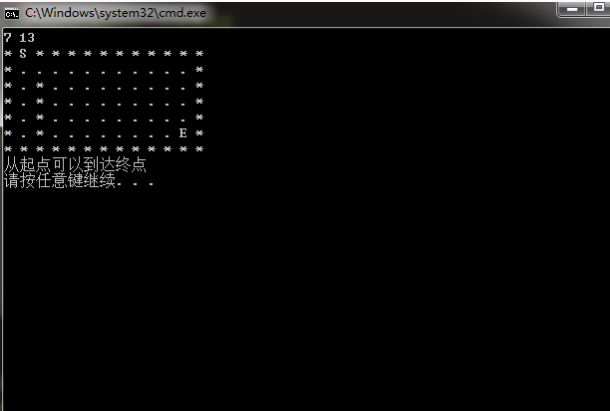
不要拘束于代码,搜索是一种思想,这只是我的代码风格…不要照抄我的,要自己去理解那个函数递归和回溯的过程。
这里还有几个细节问题。
如果要求输出路径怎么办?
很简单,开一个记录路径的数组,在函数递归的时候把这个数组也向下传递,到达终点时将这个数组输出。
什么时候要还原访问标记?
在上面的问题中,对于一个格子你只要搜索过一次,之后就不会再来了,因为你已经知道从这个格子无法到达终点。所以这种情况是不需要还原访问标记的。如果问题是输出一条最短的路径,或者是要求输出所有可行路径,那么对于之前已经搜索过的格子,下一条路径可能会再次访问,所以在回溯之后一定要将访问标记置0。
2.3 强力优化
靠纯粹的枚举所有情况来得出结论显然费时费力,实际上搜索是有非常大的优化空间的。这里详细讲一下剪枝优化,顺便提一下记忆化的优化方法。
2.3.1 DFS优化之剪枝(重要)
剪枝就是把一些显然不可能的情况排除掉,只搜索合理的方案。
我们来看一下这一道题
Σ(っ °Д °;)っHDOJ1010
简单来说就是给出一张n * m大小的地图,有一条小狗要从起点前往终点。每走一个格子花费1秒,求是否存在一条路径,使得从起点到达终点消耗的时间正好为t秒。
和之前举的例子相比,这道题就多了一个限制条件:必须恰好在t秒到达终点
枚举所有情况当然可行,但是效率过于低下,绝对会超时。所以这里就要用到剪枝的技巧了。
剪枝1:距离剪枝
如果当前位置与终点之间的欧几里得距离(就是两点水平距离和竖直距离之和)大于规定时间t的话,那么在t秒内无论怎么走都是无法到达终点的。这个时候我们应该及时返回,不再递归下去。
剪枝2:奇偶剪枝
如果当前位置和终点之间的欧几里得距离与时间t之和为奇数,同样无论如何都无法在t秒时到达终点。这个应该可以通过数学归纳法证明,最极端的情况是当前位置贴着终点的时候,显然无法在偶数秒内到达终点。
具体证明可以看这里Σ(っ °Д °;)っ奇偶剪枝
奇偶剪枝和距离剪枝不一样,它可以在DFS外面进行判断。因为我们发现当小狗移动一个单位时,时间也减少了一秒,所以它们的和的奇偶性并不会改变。所以我们在主函数进行奇偶剪枝即可。
当程序在递归时遇到以上两种情况时,应当及时返回,不再做无用功。这样,程序运行的效率就大大提高了。
参考代码如下
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn = 10;
int n, m,t;
int sx, sy, ex, ey;
int mp[maxn][maxn], vis[maxn][maxn];
int dir[4][2] = { {-1,0},{0,-1},{1,0},{0,1} };
bool flag;
int get_dis(int y, int x, int ny, int nx) { return abs(y - ny) + abs(x - nx); } //返回两点的欧几里得距离
void dfs(int y, int x, int time)
{
if (y == ey AND x == ex AND time == 0)
{
flag = true;
return;
}
if (time < get_dis(y, x, ey, ex)) return; //距离剪枝
if (flag == false)
{
for (int i = 0; i < 4; i++)
{
int ny = y + dir[i][0];
int nx = x + dir[i][1];
if (ny < 1 || ny > n || nx < 1 || nx > m || vis[ny][nx]) continue;
if (!mp[ny][nx])
{
vis[ny][nx] = 1;
dfs(ny, nx, time - 1);
vis[ny][nx] = 0;
/*注意,这里是要还原访问标记的。因为后续的路径有可能走到之前搜过的格子之上,所以我们在递归完成后
要把这个格子置0,以免影响到后续的搜索*/
}
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
char c;
while (cin >> n >> m >> t AND (n AND m AND t))
{
memset(mp, 0, sizeof(mp));
memset(vis, 0, sizeof(vis));
flag = false;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
cin >> c;
if (c == 'S')
{
sy = i;
sx = j;
}
if (c == 'D')
{
ey = i;
ex = j;
}
if (c == 'X')
{
mp[i][j] = 1;
}
}
}
int dis = get_dis(sy, sx, ey, ex);
if (t < dis || (t - dis) & 1) //奇偶剪枝 & 距离剪枝
{
cout << "NO" << endl;
continue;
}
vis[sy][sx] = 1;
dfs(sy, sx, t);
if (flag == true) cout << "YES" << endl;
else cout << "NO" << endl;
}
return 0;
}
2.3.2 DFS优化之记忆化
记忆化的核心思想就是把每次递归搜索时得到的答案记下来,本质上是一种动态规划的思想。具体实现,就是开一个数组记录当前节点搜索完成后的答案。当搜索到某个节点时,如果这个节点在之前已经被搜索过了,那么我们就可以直接获得这个答案并返回。如果这个节点没有被搜索过,那我们就从这个节点开始继续往下搜索。
具体的实现对于各种问题是不一样的,感兴趣的同学可以做一下这题,试试暴力DFS能过不,然后欢迎和我深入♂交流。
Σ(っ °Д °;)っHDOJ1078
2.4 例题
挑了几道基础的题,当然你们可以不做。
洛谷P1135
洛谷P1657
洛谷P1036
洛谷P1164
HDOJ1010
HDOJ1181
3.BFS——广度优先搜索
3.1 和深搜的区别
广度优先搜索较之深度优先搜索之不同在于,深度优先搜索旨在不管有多少条岔路,先一条路走到底,不成功就返回上一个路口然后就选择下一条岔路,而广度优先搜索旨在面临一个路口时,把所有的岔路口都记下来,然后选择其中一个进入,然后将它的分路情况记录下来,然后再返回来进入另外一个岔路,并重复这样的操作。
还有一个区别是,BFS一般靠循环来完成,DFS一般靠递归(虽然也有栈实现DFS的方式,但是不太直观)
所以维护BFS中待查找的节点,需要用到队列。队列是一种先进后出的数据结构,在C++中可以靠STL轻松实现,请大家不要害怕。具体可以看我博客另一篇文章STL——队列,也可以自己网上学习。
3.2 算法实现
同样,我们先来举个例子,生动形象地描述一下BFS的过程。
地图如下图所示,求小人到终点的最短距离。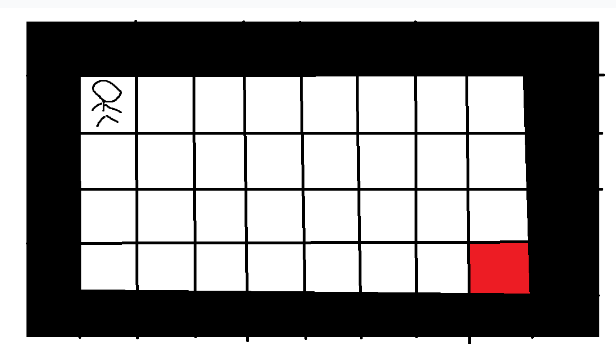
如果是DFS,那么我们就要枚举所有路径,然后选择一条路程最短的。这样有可能我们会花费大量时间在一些没用的死路里转来转去。
广搜的思路是,我们先把小人所处位置所有可行的方向都找出来,压入一个队列中,表示这些格子都是待搜索的。首先我们会把小人右边和左边两个格子标记为”1”,说明从小人从起点到这两个格子最少需要走1步。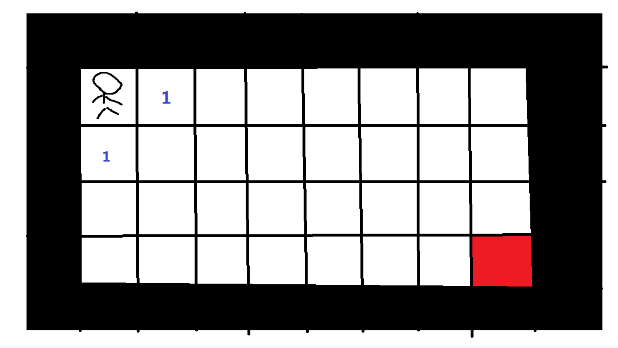
之后,我们从两个标记1的位置起,寻找可以到达的下一个位置,标记为”2”,说明小人从起点到这两个格子最少需要走2步。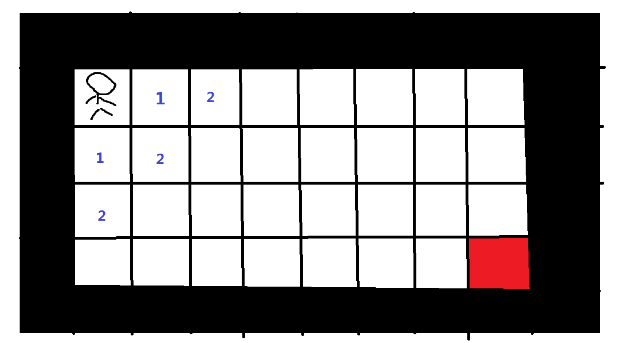
重复上面的步骤,从标记为2的位置起,寻找可到达的下一位置,标记为”3”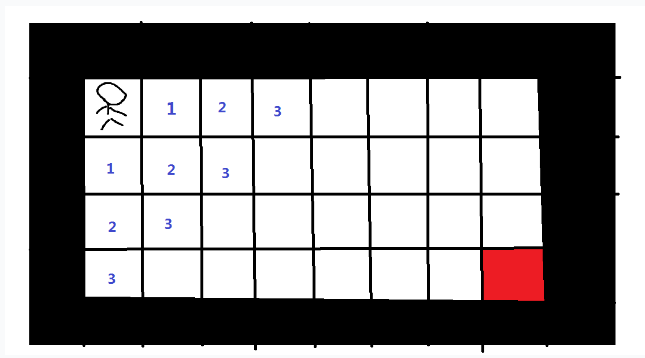
以此类推,直到某一个标记标记到了终点上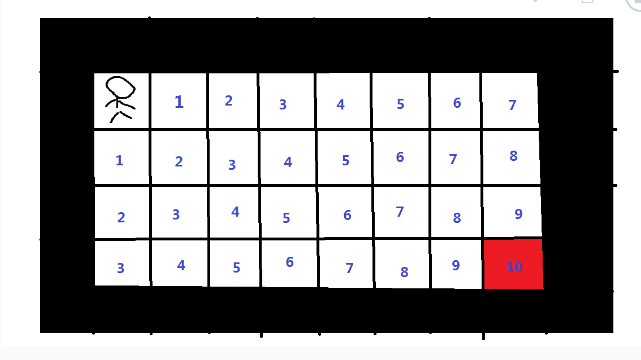
那么答案就是标记在终点上的数字:10次
这个答案可以确保是最短路径,因为在广度优先搜索中,要发现与起点距离为k+1的顶点,首先要发现所有距离为k的顶点,因此可以依次求出从起点到终点的最短距离。
下面给出代码实现的方式,首先是定义
struct Node
{
int y,x; //记录待查找节点的坐标
}
queue<Node> q; //定义队列,用于存储待查找的节点
int mp[maxn][maxn]; //存储地图
int cnt[maxn][maxn]; //记录节点的标记,默认是-1
其实我们可以把标记距离的工作放到结构体里面。对于不同的问题,Node结构体里面存的数据可以是不一样的,并不一定只有坐标(比如某些题中,还对方向有要求,那么就在结构体中开个记录方向的变量)
下面给出求最短路径的完整代码
#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn = 128;
struct Node
{
int y, x;
};
int n, m;
int sx, sy, ex, ey;
int cnt[maxn][maxn];
int dir[4][2] = { {-1,0},{0,-1},{1,0},{0,1} };
char mp[maxn][maxn];
void bfs()
{
queue<Node> q;
Node start = { sy,sx }; //先将起点坐标入队
cnt[sy][sx] = 0;
q.push(start);
while (!q.empty()) //队列非空,说明还有待搜索的节点需要搜索
{
Node f = q.front(); q.pop(); //取出队首节点
if (f.y == ey AND f.x == ex) break; //如果搜到终点了,退出循环
for (int i = 0; i < 4; i++) //遍历当前节点的四个方向
{
int ny = f.y + dir[i][0];
int nx = f.x + dir[i][1];
if (ny < 1 || ny > n || nx < 1 || nx > m || cnt[ny][nx] != -1) continue;
if (mp[ny][nx] != '*') //下一位置可走
{
cnt[ny][nx] = cnt[f.y][f.x] + 1; //下一个位置的距离为当前位置距离+1
Node next = { ny,nx };
q.push(next); //将next入队
}
}
}
}
int main()
{
while (cin >> n >> m)
{
memset(cnt, -1, sizeof(cnt)); //将cnt数组初始化为-1,代表未访问过
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
cin >> mp[i][j];
if (mp[i][j] == 'S')
{
sy = i;
sx = j;
}
if (mp[i][j] == 'E')
{
ey = i;
ex = j;
}
}
bfs();
cout << cnt[ey][ex] << endl;
}
}
3.3 BFS的限制
讲一个BFS的限制。BFS求最短路是要求每条道路的长度是一样长的,若是要求道路不一样长的地图的最短路,直接上裸BFS会出问题。解决方法是用优先队列代替普通队列,让路短的优先值高,路长的优先级低。这样可以确保访问到终点时,经过的路是最短的。
实际上求复杂图的最短路时,我们一般采用Dijkstra或者SPFA来搞,因为BFS属于暴力算法,复杂度是比较高的。
3.4 例题
其实BFS做多了会比DFS爽..
HDOJ1253
HDOJ1495
CF GYM 101502 D
4.写在结尾
对于这两个搜索方法,其实我们是可以轻松的看出来,他们有许多差异与许多相同点的。
1.数据结构上的运用
DFS用递归的形式,用到了栈结构,先进后出。
BFS选取状态用队列的形式,先进先出。
2.复杂度
DFS的复杂度与BFS的复杂度大体一致,不同之处在于遍历的方式与对于问题的解决出发点不同,DFS适合目标明确,而BFS适合大范围的寻找。
3.思想
思想上来说这两种方法都是穷竭列举所有的情况。
本文主要参考了知乎dalao @Godshi 的文章
文章链接
那么这就是本次算法授课,由于本人菜的一笔,只能做点搬运工作。上面写的都是我乱编的,各位不要过于信任我的说法。总之,不要被我繁杂的文风迷惑了,其实DFS和BFS还是很好懂的(°ー°〃)
