最小生成树

关于图的几个概念定义

• 连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。
• 强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。
• 连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
  -生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
• 最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

Prim算法

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

1. 图的所有顶点集合为V；初始令集合u={s},v=V−u;
2. 在两个集合u,v能够组成的边中，选择一条代价最小的边(u0,v0)，加入到最小生成树中，并把v0并入到集合u中。
3. 重复上述步骤，直到最小生成树有n-1条边或者n个顶点为止。

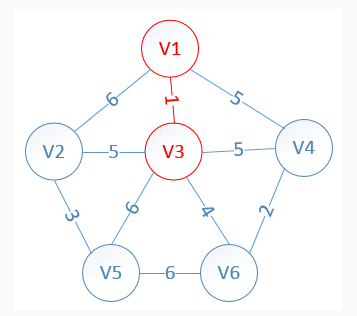
用图来演示一下
我们先定义三个数组
d[i]:记录以i为终点的边的最小权值，如果不存在，则默认为无限大
p[i]:记录在MST中，节点i的父节点。起始点p[0]为-1
color[i]:标记每一个节点的访问状态。WHITE:未访问,GRAY:等待访问,BLACK:已访问

初始状态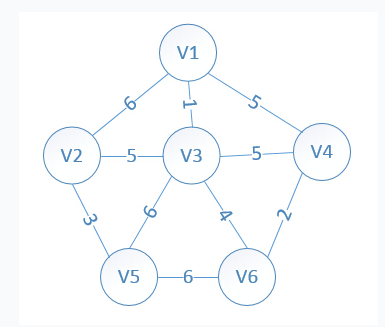

先将起始点V1加入MST，与V1相邻的点有V2，V3，V4，我们更新他们的状态。