HDOJ——1506 裸单调栈

题目链接

题目大意

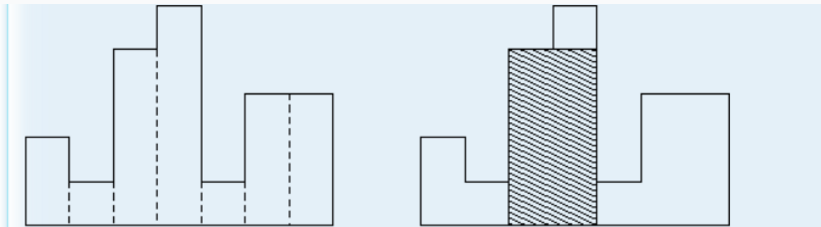
A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:
给出一个描述高度的数列，宽度为1，求能扫描出来的最大面积

分析

这道题应该有很多种解法，这里提供一个单调栈的思想。
单调栈顾名思义，就是维护一个栈，栈内元素肯定是单调上升(下降的)
单调栈可以在线性复杂度内解决求一个元素右侧/左侧出现的第一个大于它/小于它的元素的下标。
对于这道题，我们要求的是最大面积。对于每一块板子，它可以向右延伸到第一块小于它的板子，也可以向左延伸到第一块小于它的板子。对于这块板子的最大面积就是len[i] * 向左右延伸的最大长度。

实现方法

举例:在一个数列中，求每一个元素右侧的第一个小于它的元素位置。
我们定义一个栈保存元素下标，如果栈为空或者当前元素大于等于栈顶元素，就把它的下标压入栈。如果当前元素小于栈顶元素，就将栈顶元素取出，直到大于等于栈顶元素为止。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<stack>
using namespace std;
typedef long long LL;
const int maxn = 100000 + 10;
stack<int> s;
int n,num[maxn],pre[maxn],sub[maxn];
LL max(LL a,LL b){return a>b?a:b;}
int main()
{
  LL ans;
  while(cin >> n && n)
  {
    ans = 0;
    for(int i=1;i<=n;i++) cin >> num[i];
    for(int i=1;i<=n;i++)
      if(s.empty() || num[i] >= num[s.top()]) s.push(i);
      else
      {
        while(!s.empty() && num[i] < num[s.top()]){sub[s.top()] = i - s.top() - 1;s.pop();}
        s.push(i);
      }
    while(!s.empty()){sub[s.top()] = n - s.top();s.pop();}  //栈内剩下的元素可以一直延伸到栈尾
    for(int i=n;i>=1;i--)
      if(s.empty() || num[i] >= num[s.top()])  s.push(i);
      else
      {
         while(!s.empty() && num[i] < num[s.top()]){pre[s.top()] = s.top() - i - 1;s.pop();}
         s.push(i);
      }
    while(!s.empty()){pre[s.top()] = s.top() - 1;s.pop();}
    //for(int i=1;i<=n;i++) cout << i << "  " << pre[i] << "  " << sub[i] << endl;
    for(int i=1; i<=n;i++) ans = max(ans,1LL*num[i]*(pre[i]+sub[i]+1));
    cout << ans << endl;
  }
}